算法练习:【提高】过河卒【***】
信奥C++
Posted on 2023-08-22
摘要 : 使用二维数组来做判定工具。
每一个格的路线数量,都是它上面和左边2格路线数量的和。
建立数组时,如果长度是变量,则会出现变量初始数值不为零的情况,这是C++的特性。
Posted on 2023-08-22
摘要 : 使用二维数组来做判定工具。
每一个格的路线数量,都是它上面和左边2格路线数量的和。
建立数组时,如果长度是变量,则会出现变量初始数值不为零的情况,这是C++的特性。
❱ 描述
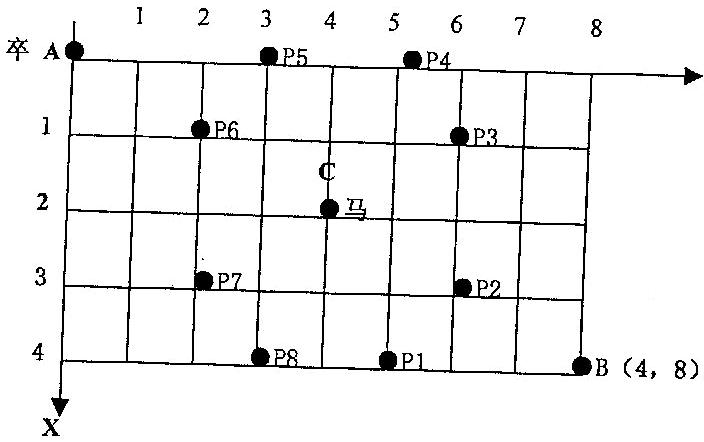
A 点有一个过河卒,需要走到目标 B
点。卒行走规则:可以向下、或者向右。同时在棋盘上的任一点有一个对方的马(如下图的C点),该马所在的点和所有跳跃一步可达的点称为对方马的控制点。例如下图
C 点可以控制 9 个点(图中的P1,P2 … P8 和 C)。卒不能通过对方马的控制点。 棋盘用坐标表示,现给定A 点位置为(0,0)B
点位置为(n,m)(n,m 为不超过 20 的整数),马的位置为C(X,Y)(约定:
C点与A点不重叠,与B点也不重叠)。要求你计算出卒从 A 点能够到达 B 点的路径的条数。
❱ 输入描述
B点的坐标(n,m)以及对方马的坐标(X,Y)(马的坐标一定在棋盘范围内,但要注意,可能落在边界的轴上)
❱ 用例输入
6 6 3 2
❱ 用例输出
17
#include<iostream>
using namespace std;
int main() {
int n,m,X,Y;
cin>>n>>m>>X>>Y;
//使用静态数值来建立数组,不容易出错。
int a[22][22] = {0};
//建立参照数组,把不能走的路线标注为1。
a[X][Y]=1;
a[X-1][Y-2] =1;
a[X-1][Y+2] =1;
a[X-2][Y-1] =1;
a[X-2][Y+1] =1;
a[X+1][Y-2] =1;
a[X+1][Y+2] =1;
a[X+2][Y-1] =1;
a[X+2][Y+1] =1;
//使用静态数值来建立数组,不容易出错。
long long r[22][22] = {0};
//从 0,0 开始赋值为1
r[0][0] = 1;
//每一个格的路线数量,都是它上面和左边2格路线数量的和。
for(int i=0;i<=n;i++){
for(int j=0;j<=m;j++){
if(a[i][j]>0 || i==0&&j==0){
continue; //跳过 数组a里的格 //跳过起点
}
if(i-1>=0){
r[i][j] += r[i-1][j];
}
if(j-1>=0){
r[i][j] += r[i][j-1];
}
}
}
cout << r[n][m];
return 0;
}
using namespace std;
int main() {
int n,m,X,Y;
cin>>n>>m>>X>>Y;
//使用静态数值来建立数组,不容易出错。
int a[22][22] = {0};
//建立参照数组,把不能走的路线标注为1。
a[X][Y]=1;
a[X-1][Y-2] =1;
a[X-1][Y+2] =1;
a[X-2][Y-1] =1;
a[X-2][Y+1] =1;
a[X+1][Y-2] =1;
a[X+1][Y+2] =1;
a[X+2][Y-1] =1;
a[X+2][Y+1] =1;
//使用静态数值来建立数组,不容易出错。
long long r[22][22] = {0};
//从 0,0 开始赋值为1
r[0][0] = 1;
//每一个格的路线数量,都是它上面和左边2格路线数量的和。
for(int i=0;i<=n;i++){
for(int j=0;j<=m;j++){
if(a[i][j]>0 || i==0&&j==0){
continue; //跳过 数组a里的格 //跳过起点
}
if(i-1>=0){
r[i][j] += r[i-1][j];
}
if(j-1>=0){
r[i][j] += r[i][j-1];
}
}
}
cout << r[n][m];
return 0;
}
#include <iostream>
#include <cstdlib>
using namespace std;
int n, m, x, y, f[23][23];
bool ok(int a, int b) {
if(a == x && b == y) return false;
if(abs(a - x) == 1 && abs(b - y) == 2) return false;
if(abs(a - x) == 2 && abs(b - y) == 1) return false;
return true;
}
int main() {
cin >> n >> m >> x >> y;
if(ok(0, 0)) f[0][0] = 1;
for(int i = 0; i <= n; i++) {
for(int j = 0; j <= m; j++) {
if(!ok(i, j)) continue;
if(i) f[i][j] += f[i - 1][j];
if(j) f[i][j] += f[i][j - 1];
}
}
cout << f[n][m];
return 0;
}
#include <cstdlib>
using namespace std;
int n, m, x, y, f[23][23];
bool ok(int a, int b) {
if(a == x && b == y) return false;
if(abs(a - x) == 1 && abs(b - y) == 2) return false;
if(abs(a - x) == 2 && abs(b - y) == 1) return false;
return true;
}
int main() {
cin >> n >> m >> x >> y;
if(ok(0, 0)) f[0][0] = 1;
for(int i = 0; i <= n; i++) {
for(int j = 0; j <= m; j++) {
if(!ok(i, j)) continue;
if(i) f[i][j] += f[i - 1][j];
if(j) f[i][j] += f[i][j - 1];
}
}
cout << f[n][m];
return 0;
}