完美十字架
❱ 描述
给定一个 n 行 n 列的矩阵,记矩阵中第 i 行第 j 列上的数为 a[i][j]。从 a[i][j] 出发,分别往上、下、左、右取 k 个数(包括 a[i][j]),得到的 4k−3 个元素被称为以 a[i][j] 为中心的十字架。
一个十字架中,从 a[i][j] 开始往右 k 个数(包括 a[i][j])的和被称为十字架的右臂和。同理可以定义十字架的左臂和、上臂和及下臂和。
下图为 k=3 时的一个十字架示例,阴影部分是它的下臂
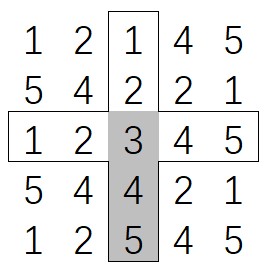
一个完美十字架的左臂和、右臂和、上臂和及下臂和都是奇数且都是 3 的倍数。请找出给定的矩阵中有多少个完美十字架
❱ 输入描述
第一行两个整数 n,k,表示矩阵的大小和十字架的大小
接下来 n 行,每行 n 个整数,表示矩阵中的元素
❱ 输出描述
一个整数,表示矩阵中完美十字架的数量
❱ 用例输入
4 2
1 2 1 2
2 1 2 1
1 2 1 2
2 4 1 1
1 2 1 2
2 1 2 1
1 2 1 2
2 4 1 1
❱ 用例输出
2
❱ 提示
样例1说明:
样例1给定的矩阵中,2个完美十字架如下图所示
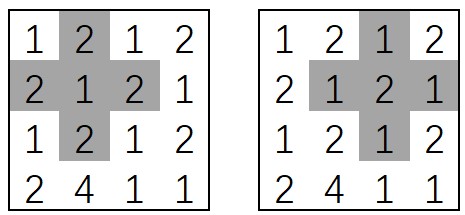
数据范围:
对于 30% 的数据,1≤n≤50,1≤a[i][j]≤1000,k=2
对于 60% 的数据,1≤n≤50,1≤a[i][j]≤1000,2≤k≤3
对于 100% 的数据,1≤n≤50,1≤a[i][j]≤1000,2≤k≤10
#include <bits/stdc++.h>
using namespace std;
int a[60][60] = {0};
int main(){
int n,k;
cin>>n>>k;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cin >>a[i][j];
}
}
int cnt=0;
int sum = 0;
for(int i=k;i<=n-k+1;i++){
for(int j=k;j<=n-k+1;j++){
//up
sum = 0;
for(int q=i-k+1;q<=i;q++){
sum += a[q][j];
//cout<<"a["<<q<<"]["<<j<<"]";
}
//cout <<"up"<<endl;
if(sum%2==0 || sum%3>0){continue;}
//down
sum = 0;
for(int q=i;q<=i+k-1;q++){
sum += a[q][j];
//cout<<"a["<<q<<"]["<<j<<"]";
}
//cout <<"down"<<endl;
if(sum%2==0 || sum%3>0){continue;}
//left
sum = 0;
for(int q=j-k+1;q<=j;q++){
sum += a[i][q];
//cout<<"a["<<q<<"]["<<j<<"]";
}
//cout <<"left"<<endl;
if(sum%2==0 || sum%3>0){continue;}
//right
sum = 0;
for(int q=j;q<=j+k-1;q++){
sum += a[i][q];
//cout<<"a["<<q<<"]["<<j<<"]";
}
//cout <<"right"<<endl;
if(sum%2==0 || sum%3>0){continue;}
cnt ++;
//cout<<cnt;
}
}
cout<<cnt;
return 0;
}
using namespace std;
int a[60][60] = {0};
int main(){
int n,k;
cin>>n>>k;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cin >>a[i][j];
}
}
int cnt=0;
int sum = 0;
for(int i=k;i<=n-k+1;i++){
for(int j=k;j<=n-k+1;j++){
//up
sum = 0;
for(int q=i-k+1;q<=i;q++){
sum += a[q][j];
//cout<<"a["<<q<<"]["<<j<<"]";
}
//cout <<"up"<<endl;
if(sum%2==0 || sum%3>0){continue;}
//down
sum = 0;
for(int q=i;q<=i+k-1;q++){
sum += a[q][j];
//cout<<"a["<<q<<"]["<<j<<"]";
}
//cout <<"down"<<endl;
if(sum%2==0 || sum%3>0){continue;}
//left
sum = 0;
for(int q=j-k+1;q<=j;q++){
sum += a[i][q];
//cout<<"a["<<q<<"]["<<j<<"]";
}
//cout <<"left"<<endl;
if(sum%2==0 || sum%3>0){continue;}
//right
sum = 0;
for(int q=j;q<=j+k-1;q++){
sum += a[i][q];
//cout<<"a["<<q<<"]["<<j<<"]";
}
//cout <<"right"<<endl;
if(sum%2==0 || sum%3>0){continue;}
cnt ++;
//cout<<cnt;
}
}
cout<<cnt;
return 0;
}