递推作业:【基础】数塔问题
信奥C++
Posted on 2023-08-19
摘要 : 二维数组,逆向思维。
有如下所示的数塔,要求从底层走到顶层,若每一步只能走到相邻的结点,则经过的结点的数字之和最大是多少?
原理:
从下往上,从 n-1 行开始,每一格,都等于下一行相邻2个中较大那个值 加上 自己本身。
所以当叠加到 a[1][1] 时,即可得出最大的步数。
Posted on 2023-08-19
摘要 : 二维数组,逆向思维。
有如下所示的数塔,要求从底层走到顶层,若每一步只能走到相邻的结点,则经过的结点的数字之和最大是多少?
原理:
从下往上,从 n-1 行开始,每一格,都等于下一行相邻2个中较大那个值 加上 自己本身。
所以当叠加到 a[1][1] 时,即可得出最大的步数。
有如下所示的数塔,要求从底层走到顶层,若每一步只能走到相邻的结点,则经过的结点的数字之和最大是多少?
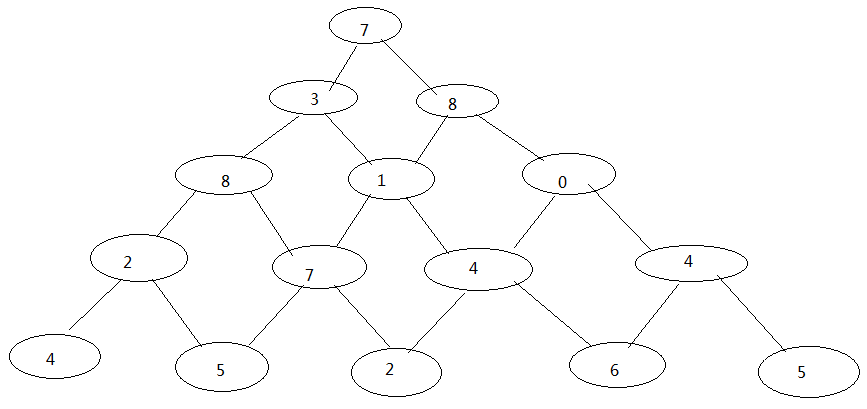
输入数据首先包括一个整数整数N(1 <= N <= 100),表示数塔的高度,接下来用N行数字表示数塔,其中第i行有个i个整数,且所有的整数均在区间[0,99]内。
从底层走到顶层 经过的数字的最大和是多少?

❱ 输入描述
输入数据首先包括一个整数整数N(1 <= N <= 100),表示数塔的高度,接下来用N行数字表示数塔,其中第i行有个i个整数,且所有的整数均在区间[0,99]内。
❱ 输出描述
从底层走到顶层 经过的数字的最大和是多少?
❱ 用例输入
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
❱ 用例输出
30
#include<iostream>
using namespace std;
int main() {
int n;
cin>>n;
int a[n+2][n+2]={0}; //初始化二维数组
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
cin >> a[i][j]; //写入数据
}
}
/*
原理:
从下往上,从 n-1 行开始,每一格,都等于下一行相邻2个中较大那个值 加上 自己本身。
所以当叠加到 a[1][1] 时,即可得出最大的步数。
*/
for(int i=n-1;i>=1;i--){
for(int j=1;j<=i;j++){
a[i][j] += a[i+1][j] > a[i+1][j+1] ?a[i+1][j]:a[i+1][j+1];
}
}
cout << a[1][1];
/*
//打印二维数组
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
cout << a[i][j];
}
cout<<endl;
}
*/
return 0;
}
using namespace std;
int main() {
int n;
cin>>n;
int a[n+2][n+2]={0}; //初始化二维数组
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
cin >> a[i][j]; //写入数据
}
}
/*
原理:
从下往上,从 n-1 行开始,每一格,都等于下一行相邻2个中较大那个值 加上 自己本身。
所以当叠加到 a[1][1] 时,即可得出最大的步数。
*/
for(int i=n-1;i>=1;i--){
for(int j=1;j<=i;j++){
a[i][j] += a[i+1][j] > a[i+1][j+1] ?a[i+1][j]:a[i+1][j+1];
}
}
cout << a[1][1];
/*
//打印二维数组
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
cout << a[i][j];
}
cout<<endl;
}
*/
return 0;
}