环形跑道追及问题【*】
问题描述:甲乙两人环缠周长是 300 米的跑道跑步,甲每秒跑 6 米,乙每秒跑 4 米,如果了两人是从同一地点同向出发,假设两人永远保持体力可以一直均速跑下去,我们知道,甲可以第一次、第二次、…、第n次这上乙。
求第n次栓到的时间 (n < 10000),单位为秒。
输入:一个整数n(n 小于等于 10000)。
输出:求第 n 次相遇的时间,单位为秒。
测试输入:1
测试输出:150
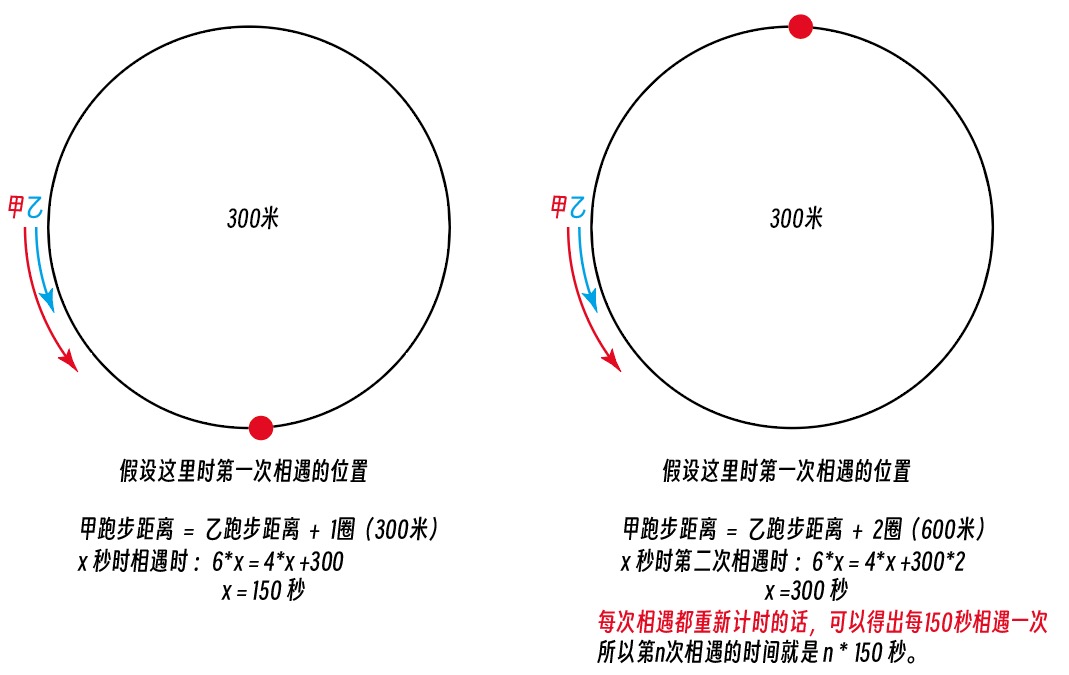
甲乙第一次相遇时,甲肯定要比乙多跑一圈,两人才能相遇。
假设这时的时间为x,那么这时:
同理,第二次相遇时,甲肯定要比多跑两圈,
由此可以看出,每次相遇都重新计时的话,可以得出每150秒相遇一次。
所以第n次相遇的时间就是 n * 150 秒。
跑道的长度、甲的速度、乙的速度都转换成变量,分别对应 s 、a、 b。
输入一行数据包含四个数值: n、s、a、b。
要求出第 n 圈所需的时间 x。
那么可以列出关系
转换一下
求第n次栓到的时间 (n < 10000),单位为秒。
输入:一个整数n(n 小于等于 10000)。
输出:求第 n 次相遇的时间,单位为秒。
测试输入:1
测试输出:150

❱
甲乙第一次相遇时,甲肯定要比乙多跑一圈,两人才能相遇。
甲跑步距离 = 乙跑步距离 + 1圈(300米)
假设这时的时间为x,那么这时:
6*x = 4*x +300
x =150 秒
x =150 秒
同理,第二次相遇时,甲肯定要比多跑两圈,
6*x = 4*x +300*2
x =300 秒
x =300 秒
由此可以看出,每次相遇都重新计时的话,可以得出每150秒相遇一次。
所以第n次相遇的时间就是 n * 150 秒。
#include <iostream>
using namespace std;
int main(){
int n;
cin >> n;
cout<<n*300/2;
return 0;
}
using namespace std;
int main(){
int n;
cin >> n;
cout<<n*300/2;
return 0;
}
❱ 升级版
跑道的长度、甲的速度、乙的速度都转换成变量,分别对应 s 、a、 b。
输入一行数据包含四个数值: n、s、a、b。
要求出第 n 圈所需的时间 x。
那么可以列出关系
甲跑步距离 = 乙跑步距离 + 跑道长度*圈数
a*x = b*x + s*n
a*x = b*x + s*n
转换一下
x = s*n/(a-b)
#include <iostream>
using namespace std;
int main(){
int n,s,a,b;
cin >> n>>s>>a>>b;
cout<< s*n/(a-b);
return 0;
}
using namespace std;
int main(){
int n,s,a,b;
cin >> n>>s>>a>>b;
cout<< s*n/(a-b);
return 0;
}